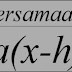Persamaan Kuadratik Dalam Bentuk Vertex

Dalam topik yang terdahulu, kita telah belajar ciri-ciri yang ada pada Persamaan Am Kuadratik. Dalam topik kali ini, kita akan belajar pula Persamaan Kuadratik dalam bentuk Vertex dan proses untuk menukar Persamaan Am Kuadratik kepada Vertex.

Apakah maksud Vertex? Vertex ialah nilai minimum atau maksimum bagi sesuatu Persamaan Kuadratik. Koordinat Vertex dinamakan juga 'Titik Pusingan'

Dalam Persamaan Vertex, koordinat (h,k) adalah titik mimimum atau maksimum bagi sesuatu graf kuadratik

Perbezaan Antara Persamaan Am Kuadratik dan Persamaan Vertex

 
Proses untuk menukar Persamaan Am Kuadratik kepada Persamaan dalam bentuk Vertex dinamakan 'Completing The Square' atau 'Penyelesaian Kuasa Dua' 

Sebelum kita pergi dengan lebih mendalam, kita perlu huraikan dahulu bagaimana Persamaan Am Kuadratik diubah kepada Persamaan Vertex menggunakan illustrasi 'Luas Segiempat'

Daripada Persamaan Am Kuadratik....

1) Faktor pemalar 'a'...kita akan dapat

 Sekarang kita fokus pada...................

2) kita illustrasikan persamaan ini menggunakan persamaan luas segiempat....

3) Pecahkan kotak berwarna oren kepada 2 bahagian. Oleh itu setiap luas kotak menjadi separuh dari yang asal.....

4) Cantumkan kotak oren yang telah dibahagi 2 kepada kotak yang berwarna pink seperti rajah di bawah

 
5) Tambahkan kotak berwarna kuning seperti rajah di bawah. Untuk menambahkan kotak kuning kepada rajah yang asal, kita perlu menseimbangkan Persamaan Am Kuadratik. Oleh itu, persamaan bertukar kepada

 6) Jika dicantumkan ketiga-tiga segiempat menjadi satu, maka persamaan telah berubah menjadi

7) Ringkaskan persamaan dengan mendarabkan nilai 'a'

8) Bandingkan dengan Persamaan Vertex

Perbezaan Antara Persamaan Am Kuadratik dan Persamaan Vertex

Maka kita akan dapati, formula untuk mendapatkan Titik Pusingan atau Vertex sesuatu Persamaan Kuadratik adalah seperti didalam jadual dibawah (h,k).

Topik Seterusnya

Persamaan Am Kuadratik

Sebelum kita belajar dengan lebih dalam dan terperinci mengenai Persamaan Kuadratik, kita kene mulakan dahulu dengan mengenali Persamaan Am Kuadratik. Persamaan Am Kuadratik adalah seperti di bawah ini dimana kuasa tertinggi bagi pembolehubah, iaitu 'X' adalah 2.

Terdapat 2 jenis bentuk Graf Kuadratik

1) Melengkung ke atas, di mana kita akan dapat nilai maksimum bagi graf tersebut adalah dipuncak graf. Bagi graf dibawah, nilai maksimum/titik maksimum bagi graf tersebut adalah 8. Perhatikan nilai 'a'..akan diulas dengan lebih mendalam..

F(x) = x²+8

2) Melengkung ke bawah dimana nilai minimum adalah berada di cerun pada rendah pada graf di bawah. Bagi graf di bawah, nilai mimimum bagi graf kuadratik tersebut adalah -8. Perhatikan nilai 'a'..akan diulas dengan lebih mendalam..

F(x) = -x²+8

Apakah itu 'a'??
Apakah itu 'b'??
Apakah itu 'c'??
Apakah itu 'x'??

Kita mulakan dulu dengan 'x'...

Sekiranya kita selesaikan persamaan kuadratik iaitu...

f(x) =0....
  
1) maka kita akan dapat nilai pembolehubah 'x'  yang melintasi paksi y=0.

2) nilai 'x' yang melintasi paksi y=0 juga dipanggil 'punca' kepada persamaan kuadratik. 

3) Oleh kerana kuasa tertinggi bagi persamaan kuadratik adalah 2, maka terdapat 2 nilai punca bagi persamaan kuadratik.

Contoh graf Persamaan Kuadratik yang mempunyai pintasan y=0 pada nilai x=-1 dan x=5

x=-1 dan x=5 dipanggil Punca Persamaan Kuadratik.
 

Bagaimana pula dengan nilai 'a'...

Bagi nilai 'a', pemalar didalam persamaan kuadratik ini menunjukkan kecapahan atau kelengkungan. Bagaimana saya tahu?...kene buat simulasi sendiri. Saya gunakan software untuk buat graf dan ubah nilai 'a' daripada -1 hingga -3

Bagi nilai 'b' pula, sukar untuk diterangkan dengan perkataan. Tetapi dengan menggunakan simulasi graf kuadratik, kita akan dapat lihat bahawa nilai 'b' membuatkan graf bergerak di sekitar paksi-x dan paksi-y di sekitar lengkungan graf. Untuk melihat simulasi perubahan nilai b, sila click gambar di bawah. Gerakkan 'slider' di website www.mathisfun.com untuk mengubah nilai 'a', 'b' atau 'c'. Anda akan melihat kesan perubahan nilai pemalar tersebut ke atas graf.

image from www.mathisfun.com

Bagaimana pula dengan nilai 'c'. Di tingkatan 3 kita semua sudah ketahui iaitu apabila x = 0, kite akan mendapat pintasan-y bagi graf tersebut. Kita lihat contoh di bawah

Topik Seterusnya......
 

Pengenalan Persamaan Kuadratik

Siapa tahu permainan paling berjaya dalam sejarah android?..Tentulah 'Angry Bird'!!

Rasanya semua org tahu pasal game Angry Bird nih..Budak kecil yang umur 2 tahun pun sekarang sudah pandai main game Angry Bird.

Tapi aper kaitan Angry Bird dengan Persamaan Kuadratik yer?

Sebelum kita lihat kaitan antara kedua-duanya, masa kita kenal dahulu apa itu Persamaan Kuadratik.

Ciri-ciri Persamaan Kuadratik:

1) Persamaan yang mempunyai nilai kuasa tertinggi bagi pembolehubah adalah '2' (dalam bahasa matematik second degree polynomial).

2) Persamaan Kuadratrik juga adalah sejenis Fungsi kerana mempunyai satu sahaja nilai 'Y' untuk setiap nilai 'X' (Diuji dengan 'Vertical Line Test'). Garisan berwarna 'biru' adalah 'vertical line' yg digunakan untuk menguji samada graf kuadratik adalah sejenis fungsi atau tidak.

3) Persamaan Kuadratik juga dipanggil sebagai ialah Persamaan Parabola.

Sekarang kita lihat pula contoh graf kuadratik di bawah ini dan kaitannya dengan game Angry Bird? Apakah yang kite boleh nampak??

masih tidak nampak..saya perincikan lagi....

                       

Kalau kita lihat pada gambarajah di atas, kita dapat lihat bahawa laluan Angry Bird Merah untuk memusnahkan musuhnya adalah sama seperti Graf Kuadratik dan ini adalah benar!!

Bukan itu sahaja, terdapat lagi contoh lain Graf Kuadratik di dalam kehidupan seharian kita. Contohnya seperti lantunan bola, lompatan ikan lumba-lumba, kolam air pancut dan banyak lagi.

Bab Seterusnya